| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 설치
- kubernetes
- IaaS
- xenserver app&desk
- microservices
- 객체지향
- fargate
- eks
- rocky
- no-param-reassign
- 오픈스택
- 젠킨스
- 가상 데스크탑 환경
- OOP
- 쿠버네티스
- 구축
- centos7
- serverless
- AWS
- app&desk
- server base computing
- 마이크로서비스
- 프로젝트
- jenkins
- openstack
- 서버 베이스 컴퓨팅
- 로키
- eslint
- sagemaker
- 머신러닝
- Today
- Total
IT
[알고리즘] 백트래킹(Backtracking)이란? (feat. DFS, 기준함수, sum of subset) 본문
백트래킹(Backtracing)의 개요
백트래킹은 구하고자 하는 해를 튜플로 나타내고 튜플에 기준 함수(한정 함수)를 적용했을 때의 결과가 최대치, 최소치 혹은 일정 조건을 만족하게끔 만들어주는 퇴각 검색 기법으로 정의된다. 백트래킹은 해답이 될 수 있는 튜플을 완성해 나아가며 그 과정에서 미완성된 튜플에 한정 함수를 적용하여 해답의 가능성이 없는 튜플들은 더이상 진행시키지 않는 방법을 사용한다. 이때 튜플을 만드는 과정에서 스택(Stack)을 사용하여 한정 함수를 만족하면 push, 만족하지 않으면 pop을 하는 방법을 사용한다. 이런 과정이 퇴각과 전진하는 것과 비슷하다 하여 퇴각 검색 기법(백트래킹, backtracking)이라 불린다.
기준 함수(한정 함수, Bounding Function)의 사용
해답이 될 수 있는 모든 벡터를 만들어 탐색하는 원시적인 접근 방법(brute force approach)은 시간과 공간의 복잡도가 증가하여 원하는 시간에 문제를 풀지 못하는 상황이 발생한다. 한정 함수는 현재 만들어진 벡터가 해답의 조건을 만족하는지 검사하는 함수를 말한다. 탐색을 하는 도중 만들어지는 벡터가 한정 함수를 만족하는 지 판단하여 해답이 될 가능성이 없는 벡터는 더 이상 진행하지 않고 다른 벡터를 진행시킨다면 경우에 따라 문제의 풀이 시간을 상당 부분 줄이는 것이 가능하다. 해답의 수가 탐색하고자 하는 완성된 벡터의 수보다 매우 적다면 한정 함수를 사용하여 탐색의 수를 줄이는 방법이 필요하며 이때 사용되는 방법에는 퇴각 검색 기법(백트래킹, backtracking)과 분기 와 한정(branch-and-bound) 방법이 있다.
Sum of Subset 문제
백트래킹은 여러 어려운 용어와 과정을 통해 진행된다. 일반화된 설명이 주를 이루지만 특정 용어나 과정의 설명에 있어 이해를 돕기 위해 Sum of Subset이라는 문제 상황을 통해 백트래킹을 바라볼 것이다.
Sum of Subset은 n개의 서로 다른 양수들이 오름차순으로 주어지고 이들의 부분 집합의 합이 m이 되는 모든 부분 집합을 찾는 문제로 집합

가 존재할 때 합이 m이 되는 S 의 부분 집합을 모두 찾는 문제 상황으로 표현할 수 있다.
예를 들어 Sum of Subset문제에서 n=4, S={5, 9, 11, 20}, m=25 라 가정하면 이때의 해답은 (5, 9, 11) or (5, 20) 이 된다.
백트래킹이란 무엇인가?
다시금 정의를 써보면 백트래킹은 구하고자 하는 해를 튜플로 나타내고 튜플에 기준 함수(한정 함수)를 적용했을 때의 결과가 최대치, 최소치 혹은 일정 조건을 만족하게끔 만들어주는 퇴각 검색 기법으로 정의된다.
백트래킹의 목표
상태 공간 트리를 DFS로 탐색하여 해결 상태에 도달하는데 있어 불필요한 탐색을 하지 않는 것을 목표로 한다.
Sum of Subset 문제에서 나올 수 있는 조합의 모든 경우의 수를 전체 탐색을 통해 확인한다면 집합

에 대해 |S| = n 일 때, 2^n 의 경우의 수를 탐색해야 한다. 즉, 시간 복잡도가 Ω(2^n) 이 되어 매우 비효율적인 탐색이 된다.
백트래킹 과정
백트래킹은 상태 공간 트리를 탐색하는 것을 전제로 한다.
(x[1], x[2], ..., x[k]) : 1~k번째 단계에서 선택된 노드들을 순서대로 튜플로 표현한다.
T(x[1], ... x[k-1]) : (x[1], ..., x[k])의 튜플의 경로가 상태 공간 트리에 속하도록 하는 모든 x[k]의 집합이다. 즉, (x[1], ..., x[k-1]) 의 경로에서 x[k-1]의 자식 노드들을 x[k]라고 한다.
이 문제에서 예시를 드는 Sum of Subset 문제는 n=4, S={5, 9, 11, 20}, m=25 라 가정한다.
1. 문제 상황을 상태 공간 트리로 표현한다.
Sum of Subset의 경우 아래 그림과 같이 집합의 각 원소의 선택 여부로 상태 공간 트리를 표현할 수 있다.
이때 명시적 제약조건은 다음과 같다.
명시적 제약 조건 : 트리의 각 노드는 0 또는 1의 값을 가진다. 이때 i번째 높이의 노드는 i번째 원소의 선택 여부를 나타내며 0은 선택하지 않음, 1은 선택함을 나타낸다.
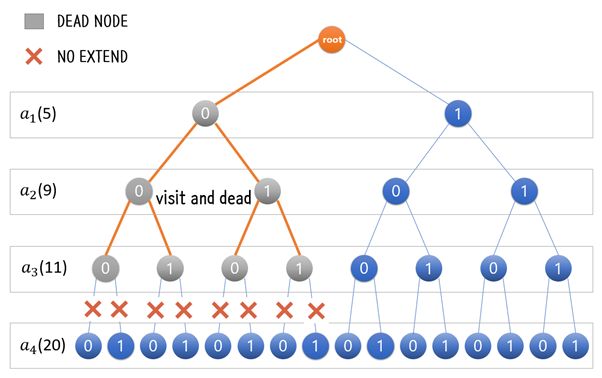
2. 루트 부터 DFS를 하여 불필요한 탐색을 하지 않고 한정 함수를 만족하는 (x[1], x[2], ..., x[n])를 찾는 것을 목표로 한다.
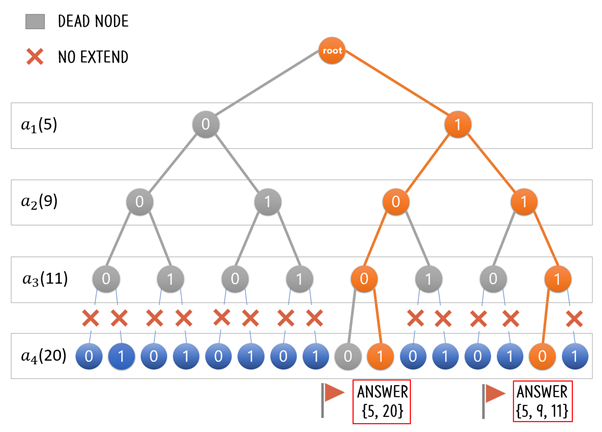
아래 [그림 2]는 Sum of Subset 문제에서 DFS 후 정답 25가 만들어지는 부분집합 {5. 25}를 찾아낸 상황이다.

3. 각 노드 s 에 도착할 때마다 루트에서 s까지의 경로 예를 들어 k번째 선택에선 (x[1], x[2], ..., x[k])의 튜플이 한정함수를 만족하는지 판단한다.
한정 함수는 암시적 제약 조건의 참/거짓 여부를 판별하는 함수이다.
Sum of Subset의 경우 집합의 원소의 개수가 n이고 원하는 부분집합의 합이 m일 때 암시적 제약 조건은 다음과 같다.
암시적 제약 조건 : w[i]를 집합에서 i번째 원소라고 가정하면 한정함수
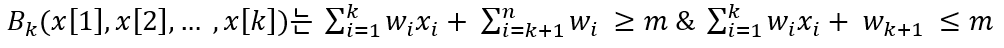
을 만족하면 참을 반환한다.

4-1. (x[1], x[2], ..., x[k])의 튜플이 한정 함수를 만족한다면 x[k] 노드를 live node이자 e-node로 변경한다.
4-2. 한정함수를 만족하지 않는 다면 T(x[1], ... x[k])의 노드들을 더이상 확장하지 않으며 dead node로 만든다.

5. k < n 일때 x[k]의 자식 노드들인 x[k+1] 들 즉, T(x[1], ... x[k])을 탐색한다.

6. 모든 자식 노드를 탐색했다면 현재 노드를 dead node로 변경한다.

7. 진행 도중 한정함수를 만족하는 (x[1], x[2], ..., x[n])에 도달하면 정답을 출력한다.

8. 정답이 도출되었거나 모든 노드가 dead 노드가 되었다면 탐색을 종료한다. 이때 정답이 여러개 인 경우에 모든 정답을 찾고 싶다면 모든 노드가 dead 노드가 될때까지 탐색해야 한다.
의사코드
위의 과정을 의사코드로 표현하면 아래와 같다.
재귀 함수를 이용한 백트래킹
백트래킹은 DFS를 하기 때문에 스택을 사용한다. 따라서 백트래킹의 단계가 깊지 않아 스택 메모리가 감당하는 한 정도라면 Recursive function 즉, 재귀 함수를 구현하는 것이 가독성 및 효율성 면에서 좋다.
backtrack(int k){
/*
T(x[1], ... x[k-1]) : (x[1], ..., x[k])의 경로가 문제 상태에 속하도록 하는 모든 x[k]의 집합
의 모든 원소에 대해 반복
*/
for each x[k] in T(x[1], ..., x[k-1]){
/*
(x[1], x[2], ..., x[k])의 경로에 대하여 한정 함수를 만족하면 x[k]를 live node이자 E-node로 만듬
*/
if(B_k(x[1], x[2], ..., x[k]) == true){
/*
(x[1], x[2], ..., x[k])가 한정함수를 만족하고 정답 노드라면 결과를 생성
*/
if(x[1], x[2], ... x[k] 가 정답 노드라면 결과 out)
/*
k가 n보다 작으면 x[k]의 자식 노드들의 활성화를 위해 backtrack(k+1) 호출
*/
if(k<n) backtrack(k+1);
/*
backtrack(k+1)를 통해 x[k]의 모든 자식 노드가 생성되었으므로
x[k]를 dead node로 만듬
*/
}
}
}
반복문을 이용한 백트래킹
하지만 백트래킹의 단계가 깊어 스택 메모리가 감당할 수 없다면 수동으로 스택의 기능을 구현하여 iterate하게 즉, 반복문을 이용하여 구현을 해야 한다.
ibacktrack(int n){
int k = 1;
while(k != 0){
/*
T(x[1], ... x[k-1]) : (x[1], ..., x[k])의 경로가 문제 상태에 속하도록 하는 모든 x[k]의 집합
의 시도하지 않은 x[k]에 대해 (x[1], x[2], ..., x[k])가 한정함수를 만족하면 x[k]를 live node이자 E-node로 만듬
이때 T(x[1], ... x[n])은 공집합이므로 바로 else로 진입함
*/
if(there remains an untried x[k] in T(x[1], x[2], ... , x[k-1])
and B_k(x[1], ... , x[k]) == true){
if(x[1], ..., x[k] 가 정답 노드라면 결과 out)
/*
x[k]의 자식 노드들의 활성화를 위해 k를 증가
*/
k = k + 1;
}else{
/*
더 이상 확인할 자식이 없거나 한정함수를 만족하는 자식이 없다면 x[k]를 dead node로 만듬
*/
k = k - 1;
}
}
}
백트래킹이 문제를 바라보는 방법
어려운 말로 정의된 백트래킹(Backtracking)을 이해하기 위해선 우선 백트래킹이 문제 상황을 어떻게 바라보고 있는지를 알아야 한다. 백트래킹은 문제 상황을 트리의 형태로 풀어나가며, 순서쌍인 튜플로 해답을 만들어낸다.
Sum of Subset 문제 상황
Sum Of Subset 문제를 예를 들어보자. 집합 S= {ai | 1≤i≤n , ai ∈N자연수} 가 존재할 때 합이 m이 되는 S 의 부분 집합을 모두 찾는 문제 상황이 존재할 때 n=4, S={5, 9, 11, 20}, m=25 라 가정하자. 이때의 해답은 {5, 9, 11} or {5, 20} 이 되며 백트래킹에서 이 문제 상황과 해답을 각각 트리와 튜플로 표현하는지 살펴보자.
문제 상황의 트리 표현
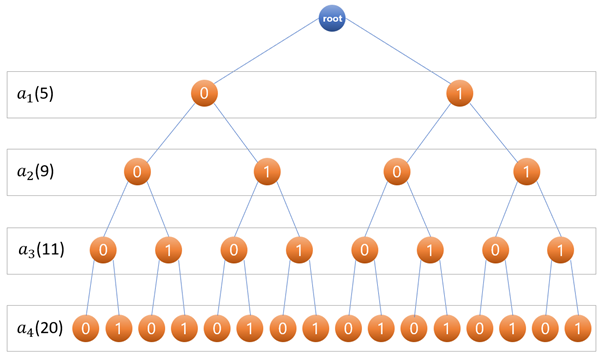
백트래킹은 위의 문제 상황을 아래 트리 형태로 표현하여 문제를 풀이한다.

각 트리의 높이를 S의 원소로 생각하고 root의 자식, 손자, 증손자... 등의 모든 노드는 해당 높이 즉, S의 원소의 선택 여부를 0(미 선택), 1(선택)로 표현한다.

예를 들어 위의 그림에서 1번 노드는 a1 을 선택하지 않은 경우 2번 노드는 a1 을 선택한 경우를 표현한다.
문제 상황의 해답 표현
백트래킹은 해답을 S의 모든 원소의 선택 여부를 표현하는 n튜플로 나타낸다.
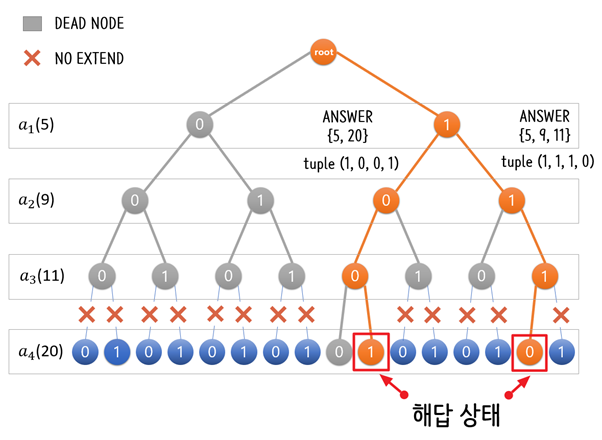
즉, 백트래킹은 위의 해답 5, 20 을 트리에서 아래 그림의 노드를 선택한 것과 같이 보고 1, 0, 0, 1 의 튜플로 표현한다.

또한, 백트래킹은 위의 해답 을 트리에서 아래 그림의 노드를 선택한 것과 같이 보고 의 튜플로 표현한다.

백트래킹 용어
Sum of Subset 문제를 통해 백트래킹 용어를 알아보도록 한다.
문제 상태(Problem State)
깊이 우선 탐색 트리의 각 노드들을 얘기한다. [그림 5]에서처럼 주황색으로 칠해진 트리의 모든 노드가 문제 상태이다.
상태 공간
루트 노드에서 다른 노드들로의 모든 경로들의 집합으로 루트에서 아래로 내려가는 순서로 루트를 제외한 노드들을 튜플로 표현한다.

명시적 제약 조건
각 단계에서 선택하는 노드들이 주어진 집합에서만 취하도록 제약하는 규칙들을 말한다. 즉, i 번째 단계에서 선택하는 노드들의 공통적인 제약 조건이라 보면 된다. 예를 들어 Sum Of Subset 문제에서 백트래킹은 주어진 집합의 i번째 원소를 선택하는가 마는가의 상황으로 인식할 수 있으므로 xi를 i번째 원소의 선택 여부라 한다면 xi, 0 or 1이 명시적 제약조건이라 할 수 있다. 아래의 [그림 7]은 이미 명시적 제약조건을 만족하는 노드들만으로 트리를 구성해 놓은 것이다.

해 공간
루트 노드에서 다른 노드들로의 명시적 제약조건을 만족하는 경로들 중 정답의 가능성이 있는 상태공간의 튜플들의 집합을 말한다. 이때 1~n까지의 단계가 있고 각 단계별로 각 높이에서 어떤 노드를 선택할지를 정하기 때문에 백트래킹에선 해 공간의 모든 튜플들의 크기가 고정되어 있다. 즉, 백트래킹에서 해 공간은 루트에서 단말 노드로의 경로 중 명시적 제약조건을 만족하는 상태공간의 튜플들의 집합을 말한다.

해 상태
문제 상태 s 중 루트에서 s로의 경로(튜플)가 해 공간의 원소가 되도록 하는 노드들을 말한다. 백트래킹에선 해 공간의 모든 튜플들의 크기가 고정되어 있으므로 해 상태는 항상 단말 노드가 된다.

암시적 제약 조건
‘i번째 단계에서 명시적 제약조건을 만족하는 노드 중 선택된 xi에 대해 루트에서 xi까지의 경로에 해당하는 상태공간들의 튜플들이 기준함수를 만족하는가’의 여부를 판단하는 조건들이다. 앞선 Sum Of Subset 문제 상황에서의 암시적 제약 조건은 아래와 같다.
암시적 제약 조건 : w[i]를 집합에서 i번째 원소라고 가정하면 한정함수

을 만족하면 참을 반환한다.
암시적 제약 조건을 만족하지 않는 경우
아래 그림과 같이 노드가 선택되었다면 상태공간의 원소 중 (0, 1, 1)의 튜플로 인해 B3(x[1], x[2], x[3]) = (20) + (20) ≥ 25 and (20) + (20) ≤ 25 의 형태로 한정 함수가 적용되며 조건
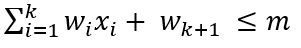
에서 (20) + (20) ≤ 25 결과로 거짓이 판명 난다. 즉, B3(x[1], x[2], x[3]) = 거짓 의 한정 함수 결과가 나타나며 이런 경우 암시적 제약 조건을 만족하지 않는다고 한다.

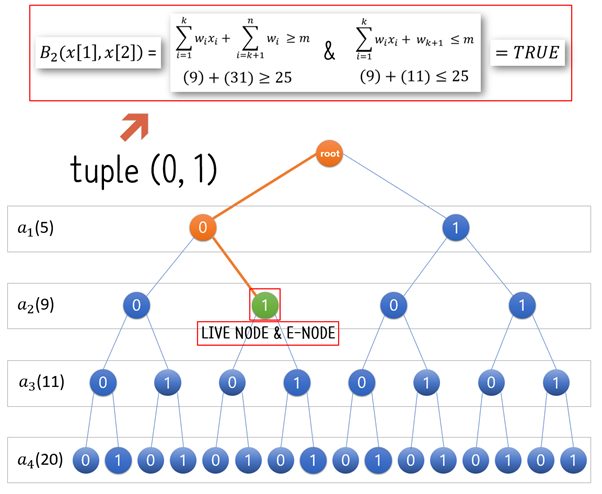
암시적 제약 조건을 만족하는 경우
아래 그림과 같이 노드가 선택되었다면 상태공간의 원소 중 (0, 1)의 튜플로 인해 B2(x[1], x[2]) = (9) + (31) ≥ 25 and (9) + (11) ≤ 25 의 형태로 한정 함수가 적용되며
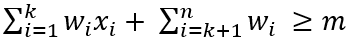
에서 (9) + (31) ≥ 25 라는 참

에서 (9) + (11) ≤ 25 라는 참이 나타나 최종 결과가 참으로 판명 난다. 즉, 참 의 한정 함수 결과가 나타나며 이런 경우 암시적 제약 조건을 만족한다고 한다.

해답 상태
해 상태 s 중 루트에서 s로의 경로(튜플)가 암시적 제약조건을 만족하는 노드들을 말한다. 앞선 Sum Of Subset 문제 상황에 정답에 해당하는 (1, 0, 0, 1)과 (1, 1, 1, 0)의 튜플 모두 암시적 제약조건을 만족하며 해 상태를 포함하게 된다. 이때의 해답 상태는 아래 [그림 11]처럼 주황색으로 칠해져 있는 부분이 된다.
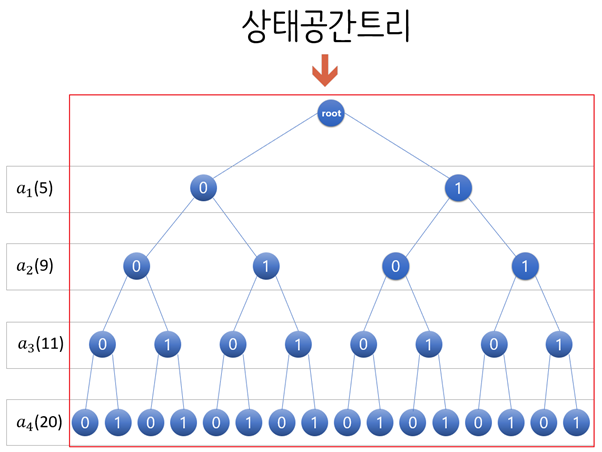
상태 공간 트리
해 공간을 통해 구성되는 트리를 말한다. 즉, 아래 [그림12]에서처럼 명시적 제약 조건을 만족하도록 백트래킹이 문제 상황을 표현한 것으로 볼 수 있다.

live node
이미 생성되었으나 아직 모든 자식 노드들이 생성 혹은 탐색되지 않은 노드이다.

E-node
현재 자식 노드들을 생성하고 있는 live node이다.

dead node
live node 중 모든 자식 노드들이 생성 혹은 탐색되었거나 한정함수를 만족하는 노드가 없어 확장되지 못한 노드를 말한다.